2016년 5월 27일 금요일

멱영행렬

멱영행렬

멱영행렬(베예쁘다 행렬, 베키제로행렬, nilpotent matrix)이란, 멱승 해 영(영행렬)이 되는 서방 행렬.즉, 어느 자연수 m에 대해서,

M m = O

하지만 성립되는 행렬 M를 말한다.멱영행렬은 기저가 주어진 벡터 공간에 대해서 멱령변환을 정한다.

목차

예

  • 영행렬은 멱영행렬이다.
  • A = \begin{pmatrix} -1 & 1 \\ -1 & 1 \end{pmatrix}, B = \begin{pmatrix} 0 & 1 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix} (은)는 각각 A2 = O, B3 = O가 되는 멱영행렬이다.
  • 실수 a, b, c에 대해서,
\begin{pmatrix} 0 & a & b \\ 0 & 0 & c \\ 0 & 0 & 0 \end{pmatrix}

의 형태를 한 행렬은 멱영행렬이다.이러한 멱영행렬 전체의 집합은, 교환자적XY-YX에 의해 리 대수(하이젠베르크군(영문판)의 리 대수)이 된다.

성질

  • 멱영행렬의 고유치는 0뿐이다.반대로, 고유치가 모두 0인 행렬은 멱영행렬이다.
  • 임의의 멱영행렬은 마사노리 행렬이 아니다.
  • N가 멱영행렬이라면, 단위행렬 I에 대해(I-N)는 마사노리 행렬이다.일반적으로, 임의의 스칼라 t에 대해서
I - (tN)^n = (I - tN) (I + tN + \cdots + (tN)^{n-1})

하지만 성립되므로, Nn = O이면 I - tN는 마사노리 행렬이다.

표준화

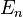E_n (을)를 n다음 단위행렬로서

N_1 = 0, N_2 = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}, N_3 = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix}, \cdots , N_n = \begin{pmatrix} 0 & E_{n-1} \\ 0 & 0 \end{pmatrix}

(와)과 두었을 때, 위의 행렬의 몇개의 곧 화(행렬을 블록으로서 대각선상에 늘어놓은 구분 행렬)

\begin{pmatrix} N_{n_1} & & 0 \\ & \ddots & \\ 0 & & N_{n_k} \end{pmatrix}

(을)를 멱영행렬의 표준형이라고 한다.여기서 n1, ... , nk는 주어진 자연수 s에 대해서 n1 + ... + nk = s를 채우는 자연수이다.

표준화의 대상이 되는 s다음 행열을 M로 했을 때,ρr = rank M r-1 - rank M r와 두면, ni = p 되는 i의 개수는 전부ρp -ρp+1개 있다.이ρi의 값에 의해서 만들어지는 멱영행렬의 표준형은, ni의 차례를 제외하고 일의적이다.이하,ρi의 값에 근거하는(s 다음) 표준형을 N[ρ1, …,ρs]라고 쓴다.또, M의 차수를 s라고 하면,ρi의 정의로부터 직접∑ρi = s가 되기 때문에, 차수 s에 있어서의 상이 되는 표준형의 개수는, 정수 s를 분할하는 방법의 개수이다.예를 들면, 차수 4에 있어서의 표준형은,

\begin{pmatrix} N_4 \end{pmatrix} , \begin{pmatrix} N_3 & 0 \\ 0 & N_1 \end{pmatrix} , \begin{pmatrix} N_2 & 0 \\ 0 & N_2 \end{pmatrix} , \begin{pmatrix} N_2 & 0 & 0 \\ 0 & N_1 & 0 \\ 0 & 0 & N_1 \\ \end{pmatrix} , \begin{pmatrix} N_1 & 0 & 0 & 0 \\ 0 & N_1 & 0 & 0 \\ 0 & 0 & N_1 & 0 \\ 0 & 0 & 0 & N_1 \end{pmatrix}

의 5이다.이 표준형은, 각각 N[1,1,1,1], N[2,1,1,0], N[2,2,0,0], N[3,1,0,0], N[4,0,0,0]이다.일반적으로 N[1, ..., 1] = (Ns), N[s, 0, ..., 0] = O가 성립한다.

Nn는, 멱승에 관해서 다음과 같은 성질을 가진다.

N_n^2 = \begin{pmatrix} 0 & N_{n-1} \\ 0 & 0 \end{pmatrix}

참고 문헌

  • 사타케 이치로 「선형대수학」쇼카보 출판사, 1974년 ISBN 978-4785313012, pp. 148 - 150, 멱영행렬의 표준형에 대해

외부 링크

「https://ja.wikipedia.org/w/index.php? title=멱영행렬&oldid=46552231」으로부터 취득

This article is taken from the Japanese Wikipedia 멱영행렬

This article is distributed by cc-by-sa or GFDL license in accordance with the provisions of Wikipedia.

Wikipedia and Tranpedia does not guarantee the accuracy of this document. See our disclaimer for more information.

In addition, Tranpedia is simply not responsible for any show is only by translating the writings of foreign licenses that are compatible with CC-BY-SA license information.

0 개의 댓글:

댓글 쓰기

피드 구독하기: 댓글 (Atom)