일반화 모멘트법

일반화 모멘트법(이파응이나 모멘트 편, 영: generalized method of moments, GMM)이란, 계량 경제학에 있어 통계 모델의 파라미터를 추정하기 위한 일반적인 방법이다.통상, 세미 파라메트릭 모델로 적용되어 그러한 세미 파라메트릭 모델에 대해 흥미가 있는 파라미터는 유한 차원이며, 한편 데이터의 분포 함수의 전모는 알려지지 않은 것도 있을 수 있다.따라서 그러한 모델로는 최우법을 적용할 수 없다.

일반화 모멘트법에 대해서는, 모델에 대한 몇개의 모멘트 조건이 특정되고 있을 필요가 있다.이러한 모멘트 조건은 모델의 파라미터와 데이터의 함수이다.예를 들면, 진정한 파라미터아래에서 기대치가 0이 되는 물건이 있다.이 때, 일반화 모멘트법은 모멘트 조건의 표본 평균이 있는 법칙을 최소화한다.

일반화 모멘트법에 따르는 추정량은 일치성, 점근정규성을 가지는 것이 알려져 한층 더 모멘트 조건 이외의 정보를 사용하지 않는 모든 추정량의 클래스에 있어 통계적으로 효율적인 일도 알려져 있다.

일반화 모멘트법은 라스・한센에 의해 1982년에, 컬・피어 손이 1894년에 도입한 모멘트법의 하나의 일반화로서 제안되었다.한센은 이 실적에 의해 2013년의 노벨 경제학상을 수상했다.

개요

이용 가능한 데이터는 T개의 관측치{Y_t } _{t = 1,..., T}로부터 되면 가정한다.여기서 각각의 관측치 Y_t는 n차원의 다차원 확률 변수이다고 한다.여기서 이 데이터는 있는 통계 모델로부터 생성된다고 해, 그 통계 모델은 미지 파라미터θ∈Θ에 의해서 정의되는 것으로 한다.이 추정 문제의 목적은 진정한 파라미터θ₀혹은 적어도 적당히 가까운 추정량을 찾아내는 것이다.

일반화 모멘트법의 일반적인 가정은 데이터 Y_t가 약정상(영문판) 한편 에르고드(영문판)인 확률 과정인 것이다(독립 한편 동일 분포에 따르는 확률 변수 Y_t는 이 조건의 특수 케이스이다).

일반화 모멘트법을 적용하기 위해, 모멘트 조건을 특정할 필요가 있다.즉 이하와 같은 벡터치 함수 g(Y,θ)가 기존이 아니면 안 된다.

m(\theta_0) \equiv \operatorname{E}[\,g(Y_t,\theta_0)\,]=0,

여기서 E는 기대치, Y_t는 일반적인 관측치를 나타낸다.더해 함수 m(θ)는θ≠θ₀이라면 0과 다른 값을 받지 않으면 안 된다.그렇지 않으면 파라미터θ는 식별 불가능하다.

일반화 모멘트법의 기본적인 아이디어는 이론적인 기대치 E[□]를 실증적인 것, 즉 표본 평균에 옮겨놓는 것이다.

\hat{m}(\theta) \equiv \frac{1}{T}\sum_{t=1}^T g(Y_t,\theta)

그리고, 이 때, 이 표현이 있는 법칙을θ에 임해서 최소화한다.법칙을 최소화하는θ이θ₀의 추정량이다.

대수의 법칙에 의해, 충분히 큰 T에 대해 $\scriptstyle\hat{m}(\theta)\,\approx\;\operatorname{E}[g(Y_t,\theta)]\,=\,m(\theta)$ 여, 따라 $\scriptstyle\hat{m}(\theta_0)\;\approx\;m(\theta_0)\;=\;0$ 가 성립되는 것이 예상된다.일반화 모멘트법은 가능한 한 $\scriptstyle\hat{m}(\;\!\hat\theta\;\!)$ 을 0에 접근하는 $\scriptstyle\hat\theta$ 을 찾는다.수학적으로는 이 방법은 $\scriptstyle\hat{m}(\theta)$ 이 있는 법칙을 최소화하는 것으로 동치이다(m의 법칙을 ||m|| (와)과 나타내, m와 제로의 사이의 거리를 측정하는 것으로 한다).결과적으로 얻을 수 있던 추정량이 가지는 성질은 법칙 함수의 선택에도 밤의 것으로, 그러므로 일반화 모멘트법의 이론은 법칙 전체의 족을 고려한다.이하를 정의한다.

\\hat{m}(\theta) ^2_{W} = \hat{m}(\theta)'\,W\hat{m}(\theta),

여기서 W는 정치정부호인 가중 행렬로 m´는 전치를 나타낸다.실천상, 가중 행렬 W는 이용 가능한 데이터 세트에 근거해 계산되어 그처럼 해 계산된 가중 행렬을 이라고 $\scriptstyle\hat{W}_T$ 한다.따라서 일반화 모멘트법에 따르는 추정량은 이하와 같이 쓸 수 있다.

\hat\theta = \operatorname{arg}\min_{\theta\in\Theta} \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\theta)\bigg)' \hat{W}_T \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\theta)\bigg)

적절한 조건아래에서, 일반화 모멘트법에 따르는 추정량은 일치성과 점근정규성을 가진다.그리고 가중 행렬 $\scriptstyle\hat{W}_T$ 을 올바르게 선택하면 효율적인 추정량이 된다.

성질

일치성

일치성이란, 추정량이 가지는 통계적인 성질이며, 충분히 많은 관측치가 있는 경우, 추정량은 진정한 값에 임의에 다가가는 것이다.

\hat\theta \xrightarrow{p} \theta_0\ \text{as}\ T\to\infty

(확률 수습을 참조).일반화 모멘트법에 따르는 추정량이 일치성을 가질 필요 충분조건은 이하와 같다.

$\hat{W}_T \xrightarrow{p} W$ (을)를 채운다.다만 W는 정치정부호 행렬이다.
$\,\theta=\theta_0$ 일 때에 한계 $\,W\operatorname{E}[\,g(Y_t,\theta)\,]=0$ 를 채운다.
파라미터가 값을 취할 수 있는 집합 $\Theta \subset \mathbb{R}^{k}$ 은 콤팩트 집합이다.
$\,g(Y,\theta)$ (은)는θ에 임해서 확률 1으로 연속이다.
$\operatorname{E}[\,\textstyle\sup_{\theta\in\Theta} \lVert g(Y,\theta)\rVert\,]<\infty$

제2의 조건(포괄적 식별 조건으로 불린다)은 자주 확인하는 것이 어렵다.비식별 문제를 조사하는데 이용되는, 필요 조건이지만 충분조건은 아닌 간단한 조건이 있다.

오더 조건 m(θ)의 차원이 적어도 파라미터 벡터θ의 차원보다 크다.
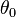
국소 식별 g(Y,θ) $\theta_0$ $W\operatorname{E}[\nabla_\theta g(Y_t,\theta_0)]$ 가의 근방에서 연속 미분 가능하다면, 행렬은 열풀 랭크이다.

실증 계량 경제학자는 실제로 포괄적 식별 조건을 확인하지 않고 , 그것이 성립하고 있으면 단지 가정하는 것이 자주 있는[¹].

점근정규성

점근정규성은 유용한 성질이며, 점근정규성에 의해 추정량의 신뢰 구간을 계산하는 것이나 가설 검정을 실시할 수 있다.일반화 모멘트법에 따르는 추정량의 점근분포에 대해 말하기 전에, 이하의 2개의 보조적인 행렬을 정의한다.

G = \operatorname{E}[\,\nabla_{\!\theta}\,g(Y_t,\theta_0)\,], \qquad \Omega = \operatorname{E}[\,g(Y_t,\theta_0)g(Y_t,\theta_0)'\,]

이하의 1에서 6까지의 조건아래에서, 일반화 모멘트법에 따르는 추정량은 점근정규성을 가진다.

\sqrt{T}\big(\hat\theta - \theta_0\big)\ \xrightarrow{d}\ \mathcal{N}\big[0, (G'WG)^{-1}G'W\Omega W'G(G'W'G)^{-1}\big]

(분포 수습을 참조).조건은 이하와 같다.

$\hat\theta$ (은)는 일치성을 가진다.
파라미터가 값을 취할 수 있는 집합 $\Theta \subset \mathbb{R}^{k}$ 은 콤팩트 집합이다.
$\,g(Y,\theta)$ (은)는 확률 1으로의 $\theta_0$ 있는 근방 N에 대해 연속 미분 가능하다.
$\operatorname{E}[\,\lVert g(Y_t,\theta) \rVert^2\,]<\infty$
$\operatorname{E}[\,\textstyle\sup_{\theta\in N}\lVert \nabla_\theta g(Y_t,\theta) \rVert\,]<\infty$
행렬 $G'WG$ 은 마사노리 행렬이다.

효율성

여기까지 행렬 W의 선택에 대해서는, 그것이 반정치정부호로 없으면 안 된다고 하는 것을 제외해 아무것도 말해 오지 않았다.실제, 어떠한 반정치정부호 행렬이어도 일반화 모멘트법에 따르는 추정량은 일치성과 점근정규성을 가진다.유일한 차이는 그 추정량의 점근분산에 있다.가중 행렬을 이하와 같이 취한다.

W \propto\ \Omega^{-1}

그러자(면), 일반화 모멘트법에 따르는 추정량은 모든 점근정규적인 추정량 중(안)에서 가장 효율적이 된다.이 경우의 효율성은, 추정량이 가능한 한 최소의 분산 행렬(있는 행렬 A가 행렬 B보다 작다고는 B-A가 반정치저부호인 것이다.)(을)를 갖는다고 하는 의미이다.

이 경우, 일반화 모멘트법에 따르는 추정량의 점근분산에 대한 공식은 이하와 같이 단순화 된다.

\sqrt{T}\big(\hat\theta - \theta_0\big)\ \xrightarrow{d}\ \mathcal{N}\big[0, (G'\,\Omega^{-1}G)^{-1}\big]

이러한 가중 행렬을 선택하는 것이 최적으로 된다고 하는 증명은, 자주 다른 추정량의 효율성을 증명할 때의 증명을 조금(뿐)만 모방한 것을 도입한다.대략적으로 말하면, 가중 행렬을 분산에 대한"샌드위치 공식"이 단순한 표현이 되도록 선택하면, 그 가중 행렬은 최적이 된다.

증명 가중 행렬을 임의의 W로 했을 때와 $W=\Omega^{-1}$ 로 했을 때의 점근분산의 차이에 대해 생각한다.만약, 그 차이가 있는 행렬 C에 대한 대칭인 적의 형식 CC' $W=\Omega^{-1}$ 로 분해할 수 있으면, 그것은 그 차이가 비부치정부호인 것을 의미해, 그러므로 정의보다는 최적으로 된다.
$\,V(W)-V(\Omega^{-1})$	$\,=(G'WG)^{-1}G'W\Omega WG(G'WG)^{-1} - (G'\Omega^{-1}G)^{-1}$
	$\,=(G'WG)^{-1}\Big(G'W\Omega WG - G'WG(G'\Omega^{-1}G)^{-1}G'WG\Big)(G'WG)^{-1}$
	$\,=(G'WG)^{-1}G'W\Omega^{1/2}\Big(I - \Omega^{-1/2}G(G'\Omega^{-1}G)^{-1}G'\Omega^{-1/2}\Big)\Omega^{1/2}WG(G'WG)^{-1}$
	$\,=A(I-B)A',$
여기서 행렬 A와 B를 기법의 단순화를 위해서 도입하고 있다.I는 단위행렬이다.행렬 B는 대칭 한편 멱등인 행렬인 것을 안다.이것은 I-B도 또 대칭 한편 멱등인 것을 의미한다.즉 $I-B=(I-B)(I-B)'$ 이 성립된다.그러므로 이전의 표현을 이하와 같이 분해하는 것이 가능하다.
	$\,=A(I-B)(I-B)'A' = \Big(A(I-B)\Big)\Big(A(I-B)\Big)' \geq 0$

실장

지금까지 말해 온 방법을 실장하는 에 해당하는 하나의 어려운 점은 W =Ω－¹으로서 가중 행렬을 취하는 것이 어려운 것이다.왜냐하면Ω의 정의보다, 그것을 계산하기 위해서는θ₀의 값이 기존이 아니면 안되어,θ₀은 확실히 미지이며, 원래 추정하려고 하고 있는 양이다.

이 문제를 해결하기 위한 방법이 몇개인가 존재한다.이하로 주는 것 쳐, 2 단계 GMM가 가장 일반적이다.

2 단계 GMM(영: Two-step GMM)

스텝 1 $\scriptstyle\hat{W}_T\;=I$ (단위행렬)으로 해, 사전의 일반화 모멘트법에 따르는 추정량 $\scriptstyle\hat\theta_{(1)}$ 을 계산한다.이 추정량은θ₀에 대한 일치 추정량이지만, 효율적은 아니다.
스텝 2

\hat{W}_T = \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\hat\theta_{(1)})g(Y_t,\hat\theta_{(1)})'\bigg)^{-1},

(으)로 한다.다만, 스텝 1에 있어서의 추정량

\scriptstyle\hat\theta_{(1)}

을 이용했다.이 행렬은Ω－¹에 확률 수습해, 그러므로 이 가중 행렬을 이용해 추정량

\scriptstyle\hat\theta

을 계산하면, 그 추정량은 점근적으로 효율적이다.

반복 GMM(영: Iterated GMM)

행렬

\hat{W}_T

을 여러 차례 계산하는 것을 제외하면, 본질적으로는 2 단계 GMM와 같은 방법이다.즉 스텝 2로 얻은 추정량을 가중 행렬로서 다시 이용해 추정량을 계산해, 이것을 반복한다.이러한 추정량은,

\scriptstyle\hat\theta_{(i)}

이라고 적지만, 이하의 시스템 방정식을 풀었을 경우와 동치가 되는[²].

\bigg(\frac{1}{T}\sum_{t=1}^T \frac{\partial g}{\partial\theta'}(Y_t,\hat\theta_{(i)})\bigg)' \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\hat\theta_{(i)})g(Y_t,\hat\theta_{(i)})'\bigg)^{\!-1} \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\hat\theta_{(i)})\bigg) = 0

이러한 반복을 실시해도 점근적인 개선은 달성할 수 없지만, 어느 몬테카를로 실험으로는 유한 표본에 있어서의 추정량의 행동이 약간 좋아지는[^{요점 출전}].

연속 갱신 GMM(영: Continuously updating GMM CUGMM 혹은 CUE)

\scriptstyle\hat\theta

(을)를 가중 행렬 W와 동시에 추정한다.즉,

\hat\theta = \operatorname{arg}\min_{\theta\in\Theta} \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\theta)\bigg)' \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\theta)g(Y_t,\theta)'\bigg)^{\!-1} \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\theta)\bigg)

(으)로서 추정한다.몬테카를로 실험에 대하고, 이 방법은 전통적인 2 단계 GMM 보다 좋은 퍼포먼스를 보이고 있다.연속 갱신 GMM는(옷자락이 두꺼워지지만, ) 중위점의 바이어스가 작아져, 그리고 많은 경우에 있어서의 과잉 식별 제약을 위한 J검정이 보다 더 누설해 있어 결과가 되는[³].

최소화의 수속의 실장에 있어서의 또 하나의 중요한 문제는, (고차원인 일도 있을 수 있다) 파라미터 공간Θ을 탐색해, 목적 함수를 최소화하는θ의 값을 찾아내는 것이 되어 있는 것이다.이러한 수속에 대해 일반적으로 추천 되는 방법은 존재하지 않고, 그것은 개개의 경우에 따르는 문제가 된다(수리 최적화).

J검정

모멘트 조건의 수가 파라미터 벡터의 차원보다 클 때, 그 모델은 과잉 식별되고 있는(영: over-identified)이라고 말한다.과잉 식별이라면, 그 모델의 모멘트 조건이 데이터와 적합할지를 조사할 수 있다.

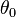개념적으로, 모델이 데이터에 자주(잘) 피트하고 있을까는, $\hat{m}(\hat\theta)$ 이 충분히 0에 가까운지 어떤지로 조사할 수 있다.일반화 모멘트법은 방정식 $\hat{m}(\theta)=0$ 을 푸는 문제, 즉 $\theta$ 이 제약을 확실히 채우도록(듯이) 선택한다고 하는 문제를 최소화 계산에 옮겨놓고 있다.이 최소화는 $m(\theta_0)=0$ 을 채우는 $\theta_0$ 이 존재하지 않는다고 해도, 항상 실행 가능하다.J검정은 이 제약이 성립하고 있을까를 확인할 수 있다.J검정은 과잉 식별 제약에 대한 검정이라고도 불린다.

이하의 통계적 가설을 생각하자.

$H_0:\ m(\theta_0)=0$ (모델이 타당하다라고 말하는 귀무가설)
$H_1:\ m(\theta)\neq 0,\ \forall \theta\in\Theta$ (모델이 타당하지 않다고 하는 대립 가설.데이터는 제약을 채우는 만큼 가까워지지 않는다.)

가설 $H_0$ 아래에서 이하의 J검정 통계량은 점근적으로 자유도 k-l의 조개 2승분포에 따른다.

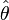J \equiv T \cdot \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\hat\theta)\bigg)' \hat{W}_T \bigg(\frac{1}{T}\sum_{t=1}^T g(Y_t,\hat\theta)\bigg)\ \xrightarrow{d}\ \chi^2_{k-\ell}

under

H_0,

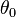여기에서는 $\hat\theta$ 파라미터 $\theta_0$ 의 일반화 모멘트법에 따르는 추정량, k는 모멘트 조건의 수(벡터 g의 차원), l는 추정 파라미터의 수(벡터θ의 차원)이다.행렬 $\hat{W}_T$ 은 $\Omega^{-1}$ 에 확률 수습하지 않으면 안 된다. $\Omega^{-1}$ (은)는 효율적인 가중 행렬이다(이전, 추정량이 효율적이기 위해서는, W는 $\Omega^{-1}$ 에 비례하는 것만이 필요했다.그러나, J검정을 실시하려면 , W는 $\Omega^{-1}$ 과 일치하지 않으면 안되어, 단순하게 비례하는 것 만으로는 안 된다).

대립 가설 $H_1$ 아래에서, J검정등 계량은 점근적으로 비유계이다.

J\ \xrightarrow{p}\ \infty

under

H_1

검정을 실시하기 위해, 데이터로부터 J의 값을 계산하지 않으면 안 된다.J는 비부이다.J를(예를 들면) $\chi^2_{k-\ell}$ 분포의95%분 정도점과 비교한다.

도 해 $J > q_{0.95}^{Ychi^2_{k-\ell}}$ 라면, 귀무가설 $H_0$ 은 유의 수준5%로 기각된다.
도 해 $J < q_{0.95}^{\chi^2_{k-\ell}}$ 라면, 귀무가설 $H_0$ 은 유의 수준5%로 기각할 수 없다.

용례

다른 많은 추정법은 일반화 모멘트법의 의미로 해석할 수 있다.

최소 이승법(영: Ordinary least squares, OLS)은 일반화 모멘트법과 이하의 모멘트 조건으로 동치가 된다.

\operatorname{E}[\,x_t(y_t - x_t'\beta)\,]=0

일반화 최소 이승법(영문판)(영: Generalized least squares, GLS)

\operatorname{E}[\,x_t(y_t - x_t'\beta)/\sigma^2(x_t)\,]=0

조작 변수법(영문판)(영: Instrumental variables regression, IV)

\operatorname{E}[\,z_t(y_t - x_t'\beta)\,]=0

비선형 최소 이승법(영: Non-linear least squares, NLS)

\operatorname{E}[\,\nabla_{\!\beta}\, g(x_t,\beta)\cdot(y_t - g(x_t,\beta))\,]=0

최우법(영: Maximum likelihood estimation, MLE)

\operatorname{E}[\,\nabla_{\!\theta} \ln f(x_t,\theta) \,]=0

실장예

참고 문헌

^ Newey & McFadden (1994, p. 2127)
^ Imbens, Spady & Johnson (1998, p. 336)
^ Hansen, Heaton & Yaron (1996)

Faciane Jr., Kirby Adam (2006), Statistics for Empirical and Quantitative Finance, Philadelphia: H.C. Baird, ISBN 0-9788208-9-4
Hall, Alastair R. (2005), Generalized Method of Moments (Advanced Texts in Econometrics), ISBN 0-19-877520-2
Hansen, Lars Peter (1982), "Large Sample Properties of Generalized Method of Moments Estimators", Econometrica 50 (4): 1029–1054, JSTOR 1912775, http://jstor.org/stable/1912775
Hansen, Lars Peter (2002), "Method of Moments", in Smelser, N. J; Bates, P. B, International Encyclopedia of the Social and Behavior Sciences, Oxford: Pergamon
Hansen, Lars Peter; Heaton, John; Yaron, Amir (1996), "Finite-sample properties of some alternative GMM estimators", Journal of Business & Economic Statistics 14 (3): 262–280, doi:10.1080/07350015. 1996.10524656, JSTOR 1392442, http://jstor.org/stable/1392442
Imbens, Guido W.; Spady, Richard H.; Johnson, Phillip (1998), "Information theoretic approaches to inference in moment condition models", Econometrica 66 (2): 333–357, JSTOR 2998561, http://jstor.org/stable/2998561
Newey, W; McFadden, D (1994), "Large sample estimation and hypothesis testing", Handbook of Econometrics, Elsevier Science
Special issues of Journal of Business and Economic Statistics: vol. 14, no. 3 and vol. 20, no. 4.

셀프피디아

일본 위키피디아 번역

2016년 5월 20일 금요일